GRE Quantitative Reasoning Typical Questions and Answers
The Free download links of GRE Quantitative Reasoning Typical Questions and Answers Papers enclosed below. Candidates who are going to start their preparation for the Graduate Record Examinations Quantitative Reasoning or Mathematics Typical papers can use these links. Download the GRE Quantitative Reasoning Typical Papers PDF along with the Answers. GRE Quantitative Reasoning Typical Papers are updated here.
A vast number of applicants are browsing on the Internet for the Graduate Record Examinations Math or Quantitative Reasoning Typical Question Papers & Syllabus. For those candidates, here we are providing the links for GRE Quantitative Reasoning Typical Papers. Improve your knowledge by referring the GRE Quantitative Reasoning Typical Question papers.

Typical Questions and Answers on Quantitative Reasoning
Directions for questions 1 to 15: Answer the questions independently of each other.
1. If f(x)=\left| \frac{1+x}{1-x} \right|, then what is the range for values of x and y for f(x)+f(y)=\frac{2(x-y)}{(1-x)(1-y)}?
(a) -1 < x < 1 ; -1 < y < 1
(b) x < -1; -1 < y < 1
(c) -1 ≤ x < 1; y ≤ -1 or y > 1
(d) x < -1; y < -1
2. Let f(x, y, z) = max{max(x, y), min(y, 2), max(z, x)}
g(x, y, z) = min{max(x, y), max(y, z), min(z, x)}
h(x, y, z) = min{min (x, y), max(y, z), max(z, x)}. x, y and z are all positive.
Which of the following is necessarily true?
(a) \frac{g(x,y,z)-h(x,y,z)}{f(x,y,z)}>0
(b) \frac{g(x,y,z)}{h(x,y,z)}>1
(c) \frac{f(x,y,z)}{h(x,y,z)}<1
(d) None of these
3. There are 8 boys — A, B, C, D, E, F, G and H. 100 ten paise coins are to be distributed among them in the above order in such a way that the distribution forms an A.P. Find the total number of coins received by C and F.
(a) 25
(b) 30
(c) 35
(d) 24
4. What is the remainder of \frac{(10^{25}-7)}{11}?
(a) 10
(b) 7
(c) 3
(d) 5
5. Two circles of radii 3 cm each are touching each other externally as shown in the figure.
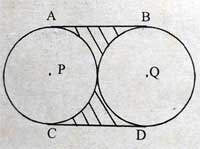
AB and CD are common tangents to both the circles. Find the area of the shaded region.
(a) 21.77 cm^{2}
(b) 7.64 cm^{2}
(c) 7.74 cm^{2}
(d) 7.84 cm^{2}
6. A circular coin of radius 1 cm is surrounded by as many circular coins as possible, of radii 1 cm each such that each of them touches the central coin. Finally, a big circular fence is laid around this combined structure such that it touches all the coins that surround the innermost coin. Black paint is poured uniformly on this structure so as to colour the coins. How much paint is wasted as a percentage of the paint not wasted?
(a) 28.57%
(b) 14.28%
(c) 22.22%
(d) None of these
7. How many different words can be formed using the letters of the word DEDICATION, such that the words never start with D?
(a) 2 x 9!
(b) \frac{10!}{4}
(c) 8! x 6
(d) \frac{96}{4}
8. In \Delta ABC, \angle A, \angle B and \angle C are in G.P. in that order. Measure of \angle B is 60°. What is the perimeter of the triangle if its height is 3 cm?
(a) \frac{3\sqrt{3}}{4} cm
(b) 6\sqrt{3} cm
(c) 3\sqrt{3} cm
(d) None of these
9. What can be the value of ‘\theta’, if (1+2\sqrt{2})\cos\theta-\sqrt{2}cos^{2}\theta=2 and \theta lies between \frac{-\pi}{2} and \frac{\pi}{2}?
(a) \frac{-\pi}{3}
(b) \frac{\pi}{3}
(c) \frac{\pi}{4}
(d) \frac{\pi}{6}
10. What is the value of \frac{x}{1+\frac{1}{1-\frac{1}{1+x}}}+\frac{x}{x+\frac{x}{x-\frac{x}{1+x}}}?
(a) \frac{x^{2}+x+1}{x+1}
(b) \frac{x^{2}}{x^{2}+x+1}
(c) 1
(d) \frac{x^{2}+x+1}{2x+1}
| Pratice Papers | Important Questions |
| Advance Questions | Previous Papers |
| Mock Test | Sample Papers |
| Typical Papers | Model Set |
11. An athlete jogging on a circular track starts from a point ‘A’ and after reaching a certain point ‘B’ runs to the centre of the circle along which the track is and then comes back to the starting point A, taking the shortest route in both the cases. He runs along the curved path i.e., arc AB at 5 kmph and along the straight route at 2 kmph. If the radius of the track is 50 m and the angle subtended by arc AB at the centre is 120° then find the time taken by the athlete to run the path. (pi: =3.14)
(a) 3.46 minutes
(b) 4.32 minutes
(c) 6.24 minutes
(d) 4.26 minutes
12. What is the value of \log_{x^{3}}(a+b)+\log_{x^{12}}(a+b)+\log_{x^{30}}(a+b)+\log_{x^{60}}(a+b)+... upto n terms?
(a) \frac{n(n+1)(2n+1)}{6}
(b) \frac{n(n+1)(n+2)}{(n+3)}\log_{x}(a+b)
(c) \frac{n(n+3)}{(n+2)}\log_{x}(a+b)
(d) \frac{n(n+3)}{2(n+1)(n+2)}\log_{x}(a+b)
13. In how many ways can 9 different balls, 5 of which are white and rest black, go into a box, if exactly 3 of the white balls have to go into the box?
(a) 10
(b) 40
(c) 126
(d) 160
14. \Delta ABC is inscribed in a circle with centre O and radius 1 cm. If \Delta ABC is an equilateral triangle, find the area of the shaded region.
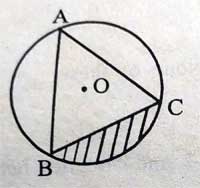
(a) 0.521 cm^{2}
(b) 0.614 cm^{2}
(c) 0.433 cm^{2}
(d) 0.157 cm^{2}
15. AO = 4 cms and AC = 4\sqrt{3} cms. O is the centre of the circle \angle AOB = 120°. Find the area of shaded region (in cm2).

(a) 8\sqrt{3} cm^{2}
(b) 4\sqrt{3} cm^{2}
(c) 12\sqrt{3} cm^{2}
(d) None of these
Directions for questions 16 to 18: Answer the questions on t-he basis of the information given below.
There are two concentric circles such that the width of the annulus is 2 cm. Also, the ratio of the areas of the two circles is 9 : 16. Then:
16. What is the area of the inner circle?
(a) 9π sq. cm
(b) 18π sq. cm
(c) 36π sq. cm
(d) 48π sq. cm
17. What is the area of the outer circle? ‘
(a) 4π sq. cm
(b) 8π sq. cm
(c) 16π sq. cm
(d) 64π sq. cm
18. What is the ratio of the circumferences of the two circles?
(a) 2:3
(b) 1:2
(c) 3:2
(d) None of these
Directions for questions 19 to 20: Answer the questions independently of each other.
19. The size of a block of Wood is 12 cm x 15 cm x 10 cm. How many such blocks, when placed together either adjacent to each other or above each other with the same orientation, can form the smallest possible solid wooden cube?
(a) 100
(b) 15
(c) 120
(d) 60
20. PQRS is a trapezium, in Which PQ is parallel to RS and PQ = 3RS. The diagonal of the trapezium intersect each other at X, then the ratio of the areas of \Delta PXQ and \Delta RXS is:
(a) 6:1
(b) 3:1
(c) 9:1
(d) 7.1



