GRE Quantitative Reasoning Model Questions and Answers
The Free download links of GRE Quantitative Reasoning Model Questions and Answers Papers enclosed below. Candidates who are going to start their preparation for the Graduate Record Examinations Quantitative Reasoning or Mathematics Model papers can use these links.
Download the GRE Quantitative Reasoning Model Papers PDF along with the Answers. GRE Quantitative Reasoning Model Papers are updated here. A vast number of applicants are browsing on the Internet for the Graduate Record Examinations Math or Quantitative Reasoning Model Question Papers & Syllabus.
For those candidates, here we are providing the links for GRE Quantitative Reasoning Model Papers. Improve your knowledge by referring the GRE Quantitative Reasoning Model Question papers.

Model Questions and Answers on Quantitative Reasoning
Directions for questions 1 to 4: Answer the questions independently of each other.
1. What is the number of zeros at the end of 150!?
(a) 30
(b) 35
(c) 37
(d) 40
2. If x, 2x + 2, 3x + 3, …… are in G.P, then the fourth term is:
(a) 27
(b) -27
(c) 13.5
(d) -13.5
3. Find the sum of the infinite series:
\frac{\log ab}{\log x} + \frac{\log ab}{\log x^{2}} + \frac{\log ab}{\log x^{4}} + \frac{\log ab}{\log x^{8}} + …
(a) \frac{\log ab}{\log x}
(b) \frac{2\log ab}{\log x}
(c) \frac{\log ab}{\log (a+b)}
(d) Can not be determined
4. If any square ABCD, the diagonals AC and BD intersects at a point X. If E, F, G and H are the midpoints of AX, BX, CX and DX respectively, then what is the ratio of (EF + FG + GH + HE) to (AD + DC + CB + BA)?
(a) \frac{1}{2}
(b) \frac{3}{2}
(c) \frac{3}{4}
(d) Data insufficient
Directions for questions 5 to 9: Each of these questions is followed by three statements. You have to study the questions and the statements and decide which of the statements is/are sufficient to answer the question.
5. Find a^{2} + b^{2} + c^{2}
I. c is mean of a and b.
II. Geometric mean of a and b is 2.
III. a^{2} + b^{2} = 17
(a) I and II only
(b) II and III only
(c) I and III only
(d) I, II and III
6. If distinct lines passing through at least 2 points are drawn using 4 coplanar points, find the number of such lines.
I. One of the points is the centroid of a triangle drawn using the remaining three points.
II. No three points are colinear.
III. All the four points lie on two intersecting lines.
(a) I only
(b) II only
(c) I or II or III
(d) I or II
7. Is x>0?
I. x^{2} – 2x – 3 = 0
II. |x + 1| = 4
III. x^{2} = 9
(a) I and II
(b) II and III
(c) I and III
(d) Any two of I, II and III
8. If x is positive. Is \sqrt[3]{x} > \sqrt[2]{x}?
I. x>0.5
II. 6x^{2} – 5x + 1 = 0
III. x < 2
(a) I or II
(b) I and II
(c) I or III
(d) Only II
9. At what time will a train reach point a, if it travel at an uniform speed and does not stop in between point B and point A?
I. The length of the train is 200 meters and it crosses a pole in 30 seconds.
II. It crosses on its way, a 400 meters long tunnel in 30 seconds.
III. The distance between point A ns point B is 120 km and the train departs from B at 1.15 p.m.
(a) I and III
(b) I, II and III
(c) I and III or II and II and III
(d) II and III
| Pratice Papers | Important Questions |
| Advance Questions | Previous Papers |
| Mock Test | Sample Papers |
| Typical Papers | Model Set |
Directions for questions 10 to 20: Answer the following questions independently of each other.
10. if α and β are roots of ax^{2} – 2bx + c = 0 then, α^{3}β^{3} + α^{2}β^{3} + α^{3}β^{2} is:
(a) \frac{c^{2}(c+2b)}{a^{3}}
(b) \frac{bc^{3}}{a^{3}}
(c) \frac{c^{2}}{a^{3}}
(d) None of these
11. Which graph represents the curve y=x?
(a) 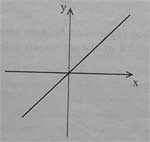
(b) 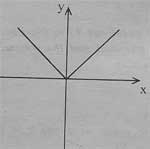
(c) 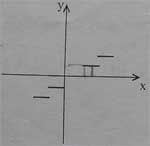
(d) 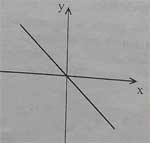
12. The centers C1, C2 and O of the three circles lie on a straight line as shown in the figure. The two larger circles have radius of 5cm each. Find the area of the smaller circle if C1C2 = 8cm
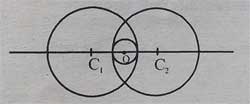
(a) \frac{\pi}{4} cm^{2}
(b) π cm^{2}
(c) 2π cm^{2}
(d) 4π cm^{2}
13. Find the greatest 5 digit number, which on being divided by 5, 6, 7, 8 and 9 leaves 3, 4, 5, 6 and 7 respectively as the reminders.
(a) 93240
(b) 98278
(c) 93249
(d) 99261
14. What is the value of \frac{(x-1)(2x + 1 - \sqrt{3}i)(2x + 1 + \sqrt{3}i)}{4}
(a) x^{3} – 1
(b) x^{3} + x^{2} – 2
(c) x^{3} + x^{2} +x -3
(d) x^{3} + \sqrt[]{3}x - (1 - \sqrt[]{3})
15. The first term of two A.P is 5. What is the ratio of their fourth terms, if the common difference of the first A.P is square of that of the second A.P and vice versa?
(a) 1:1
(b) 1:2
(c) 2:5
(d) None of these
16. If pqr = 1 then \frac{q}{q + pq + 1} + \frac{r}{r + qr + 1} + \frac{p}{p + pr + 1} is:
(a) \frac{1}{pq}
(b) pq
(c) \frac{3}{1 + pq + q}
(d) 1
17. If P represents a number between 3 and 6 and Q represents a number between 15 and 60, then \frac{Q}{P} represents a number between:
(a) 2.5 and 20
(b) 5 and 10
(c) 5 and 20
(d) 2.5 and 10
18. if f(x) = 2x + 3 and g(x) = 2x^{2} + 7x – 9, find the value of f(g(x)) when x=2.
(a) 7
(b) 17
(c) 21
(d) 29
19. P(-5, 5), Q(-4, 8), R(4, 5) and S are four points such that square PQRS forms a parallelogram . S has co-ordinates:
(a) (4, 3)
(b) (3, 2)
(c) (2, 5)
(d) None of these
20. P and Q are real numbers satisfying the conditions -4 < P < -2 and 9 > Q > -6. Which of the following expressions takes the least value?
(a) P^{2}Q
(b) PQ^{2}
(c) P^{3}Q
(d) 6PQ



