GMAT Math Previous Year Questions and Answers
The Free download links of GMAT Math Previous Year Questions and Answers Papers enclosed below. Candidates who are going to start their preparation for the Graduate Management Admission Test Math or Mathematics Previous Year papers can use these links. Download the GMAT Math Mathematics Previous Year Papers PDF along with the Answers.
GMAT Quantitative Reasoning Previous Year Papers are updated here. A vast number of applicants are browsing on the Internet for the Graduate Management Admission Test Math or Quanto Previous Year Question Papers & Syllabus. For those candidates, here we are providing the links for GMAT Quantitative Reasoning Previous Year Papers. Improve your knowledge by referring the GMAT Math Previous Year Question papers.

Previous Year Questions and Answers on Math for GMAT
Directions for questions 1 to 4: Answer the questions on the basis of the information given below
f(x)=x^{3}-7x^{2}+21x-27 ( x > 0 )
=x^{3}+8 ( x ≤ 0 )
g(x)=x^{2}-4x-21 ( x > -1 )
=\left| x \right|-x ( x < -2 )
=-\frac{1}{2}\left| x \right| Otherwise
1. If x is a positive real number and f(x) = 0, find g(x).
(a) 0
(b) -24
(c) -33
(d) Cannot be determined
2. If gof(x) = -21, find x if x is a positive natural number.
(a) 3
(b) -4
(c) +4
(d) -3
3. For what positive value of x is gof(x) = 0?
(a) 0
(b) 1
(c) -22
(d) None of these
4. If f(x)=\frac{37}{8} for x < 0, find the value of g(x).
(a) -\frac{3}{4}
(b) \frac{3}{2}
(c) 0
(d) Cannot be determined
5. If fog = -56, find the possible value of x.
(a) 2
(b) 2+\sqrt{21}
(c) 2-\sqrt{21}
(d) None of these
Directions for questions 6 and 7: Answer the questions on the basis of the information given below.
\square ABCD is a cyclic quadrilateral.
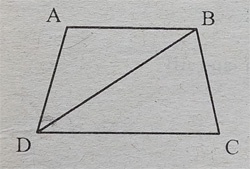
Given that \angle ADB + \angle DAB = 120° and \angle ABC + \angle BDA = 145°
6. Find the value of \angle CDB.
(a) 75°
(b) 115°
(c) 35°
(d) 45°
7. Find the value of \angle DBC.
(a) 45°
(b) 40°
(c) 35°
(d) Cannot be determined
Directions for questions 8 to 17: Answer the questions independently of each other.
8. Aqua regia is a mixture containing 50% concentrated HCL and 70% concentrated HNO3 in the ratio 1 : 3 respectively. Aqua regia is to be formed with 15L of HCL of 80% concentration and 56L of HNO3 of 90% concentration by adding water as a diluting agent. Another mixture ‘X’ having 40% concentrated HCL and 30% concentrated H2SO4 in the ratio 5 : 7 respectively is added to the Aqua regia to form a solution of 111L. Find the ratio of HCL to water in the solution. Only water is used a diluting agent.
(a) 3:8
(b) 4:7
(c) 1:3
(d) 2:5
9. Eight people, A, B, C, D, E, F, G and Hare sitting around a circular table numbered 1 to 8 in a clockwise order. A and F sit together. B and D never sit adjacent to each other. H and G sit opposite each other. What is the total number of ways in which these people can be seated?
(a) 1280 ways
(b) 2560 ways
(c) 5040 ways
(d) None of these
10. A man is standing at a base of four-storey building facing a skyscraper. He sees a lift at the 4th floor of the skyscraper at an angle of elevation of 30° and the distance between lift and man is 15 m. Then the same man goes on the top of the four-storey building and sees the lift at the top of the skyscraper at an angle of elevation of 60°.
Find the number of floors of the skyscraper if man’s height is considered negligible. (Consider the height of each floor to be same for both the buildings.)
(a) 12
(b) 10
(c) 16
(d) 20
| Practice Set | Important Question |
| Advance Questions | Previous Papers |
| Mock Test | Sample Paper |
| Typical Questions | Model Set |
11. In \Delta ABC, \angle A = 45°. B1 and B2 are two points on side AB such that AB1 and AB2 are of lengths c1 and c2 respectively and CB1 = CB2. Find \cos\angle B1CB2.
(a) \frac{2c_{1}c_{2}}{c_1^{2}+c_2 ^{2}}
(b) \frac{2c_{1}c_{2}}{c_{1}^{2}+c_{2}^{2}}
(c) \frac{c_{1}^{2}+c_{2}^{2}+b^{2}}{2(c_{1}^{2}+c_{2}^{2})}
(d) None of these
12. If 2x – 1 is an odd number and 3y – 1 is an even number, which of the following is/are necessarily even?
I. x^{2}-2y+2
II. y^{2}-2x+3
III. 4x^{2}-y-1
(a) I only
(b) II only
(c) I & II
(d) II and III
13. What is the value of x, if
\frac{1}{\log_{\frac{442}{441}}x}+\frac{1}{\log_{\frac{443}{442}}x}+\frac{1}{\log_{\frac{444}{443}}x}+ ... + \frac{1}{\log_{\frac{899}{898}}x}+\frac{1}{\log_{\frac{990}{899}}x}=2(a) \frac{2}{11}
(b) \frac{7}{10}
(c) 1
(d) \frac{10}{7}
14. ABCDEF is a regular hexagon with each side ‘X’. \square GHIJ is a rectangle inscribed inside the hexagon as shown. If BG = AG and BC || IJ, find the area of the shaded region.
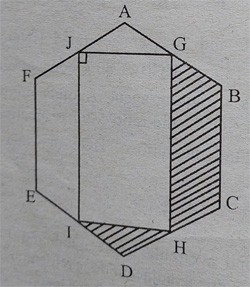
(a) \frac{3\sqrt{3}}{2}x^{2}
(b) \frac{3\sqrt{3}}{4}x^{2}
(c) \frac{3\sqrt{3}}{8}x^{2}
(d) \frac{3\sqrt{3}}{\sqrt{2}}x^{2}
15. Find the area enclosed between the x-axis and the function:
y = – x – 6; – 6 < x ≤ – 4
y = \frac{x}{2}; -4 < x < 4
y= 6 – x; 4 ≤ x ≤ 6
(a) 18
(b) 16
(c) 10
(d) 12
16. Seven friends go to an electronics shop and buy items worth Rs.500, Rs.600, Rs.800, Rs.1500, Rs.1200, Rs.1600 and Rs.l800. They are carrying only l00—rupee notes. If they are allowed to borrow and lend money from one another and the total money they have is exactly the amount required to buy these items, what is the total number of different ways they can contribute to the total money?»
(a) 486351200
(b) 5373200880
(c) 6384168200
(d) None of these
17. If \sin\theta=x, (\frac{-\Pi}{2}\lt \theta\lt \frac{\Pi}{2}) and 16x^{4}-8\sqrt{3}x^{3}-24x^{2}+18x+12\sqrt{3}-9\sqrt{3}\lt 0, then which of the following best represents x?
(a) 0\lt x\lt \frac{1}{\sqrt{3}}
(b) -1\lt x\lt \frac{\sqrt{3}}{2}
(c) \frac{\sqrt{3}}{2}\lt x\lt \frac{3}{2}
(d) -1\lt x\lt \frac{3}{2}
Directions for questions 18 to 20: Answer the questions on the basis of the information given below.
There is a circular dart board of radius 4 cm which is fitted on a square frame of side 8 cm. Three people Ajay, Vijay and Sujay are trying to hit the dart board. If you hit the centre of the dart board (bull’s eye), you get 25 points. If you hit the layer immediately outside the bull’s eye till a radius of 2 cm, you get 10 points and for hitting the outermost ring, you get 10 points. For hitting outside the dart board but inside the square frame you get 5 points. Probability of Ajay hitting within the square is \frac{1}{4}, Vijay is \frac{3}{5} and Sujay is \frac{3}{20}. Area of the bull’s eye is 1 cm2.
18. What is the probability of Ajay hitting the layer immediately outside the bull’s eye?
(a) \frac{1}{4}
(b) \frac{4\Pi-1}{256}
(c) \frac{4\Pi-1}{64}
(d) Cannot be determined
19. What is the probability of Vijay hitting the bull’s eye?
(a) \frac{3}{5}
(b) \frac{3}{320}
(c) \frac{3}{64}
(d) Cannot be determined
20. What is the probability of Sujay hitting the outermost ring of the dart board?
(a) \frac{3}{20}
(b) \frac{36\Pi}{220}
(c) \frac{9\Pi}{320}
(d) Cannot be determined



